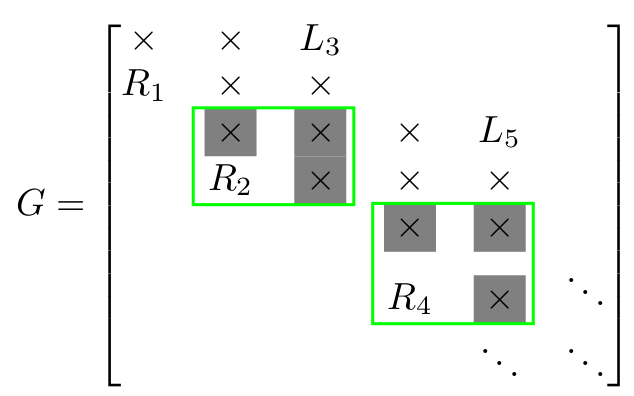
In some linear algebra problems, the involved matrices have certain blocks of low rank; for instance, quasiseparable/semiseparable matrices. These structures can be used to design faster algorithms, reducing the cost of many linear algebra operations from $\mathcal{O}(n^3)$ to $\mathcal{O}(n^2)$.
The current research focuses on expanding the scope of these algorithms, and at the same time improve their stability.
